modulus of complex number (absolute value)
When we express a distance as +10 meters. it denotes both the length of the distance and its direction. Similarly, when we express it as -10 meters, it signifies the length of the distance but in the opposite direction to +10 meters. However, when we refer to the absolute value of \(\left|10\right|\), it only represents the distance from the starting point to the ending point, regardless of direction, or if we are not certain about it’s direction.
The modulus of complex number is also known as the absolute value of the complex number. This distance is calculated using the Pythagorean theorem, considering the complex number Z = a + ib, with the real part ‘a’ as the horizontal distance and the imaginary part ‘b’ as the vertical distance, we find \(\left|\mathrm Z\right|=\sqrt{\mathrm a^2+\mathrm b^2}\) as the modulus of complex number Z.
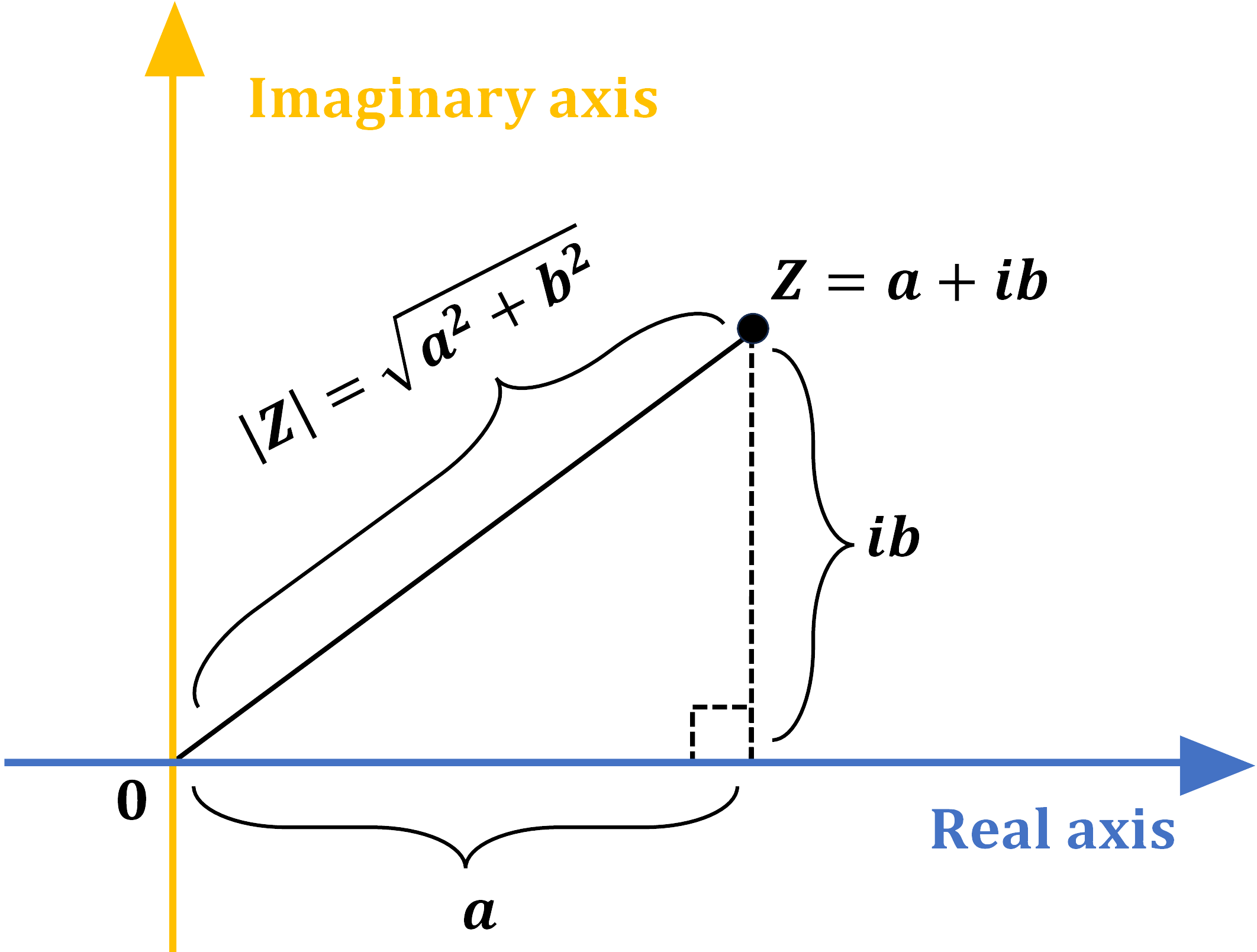
Geometrical representation of complex number
Why do we take ‘b’ instead if ‘ib’ as the imaginary part to find the absolute value of a complex number?
Geometrically, the imaginary part ‘ib’ represents a 90° rotation of the real number ‘b’ from the real axis to the imaginary axis in the complex plane. On the other hand, the absolute value of a complex number doesn’t concern itself with rotation, angles, or any transformations; it only cares about the magnitude or length from where the complex number starts to where it ends. Because of this, we do not consider ‘ib’ when finding the absolute value of a complex number.
Properties of modulus of complex number and its proofs
\((\mathrm i)\;\left|\mathrm Z\right|=\left|\overline{\mathrm Z}\right|\) \((\mathrm{ii})\;\left|\mathrm Z\right|=0\;\mathrm{if}\;\mathrm Z=0\)
\((\mathrm{iii})\;\left|\mathrm Z.\mathrm W\right|=\left|\mathrm Z\right|.\left|\mathrm W\right|\) \(\displaystyle(\mathrm{iv})\;\left|\frac{\mathrm W}{\mathrm Z}\right|=\frac{\left|\mathrm W\right|}{\left|\mathrm Z\right|}\;\mathrm{if}\;\left|\mathrm Z\right|\neq0\)
\((\mathrm v)\;\mathrm Z.\overline{\mathrm Z\;}=\left|\mathrm Z\right|^2\) (which gives absolute value of complex number using Conjugate of complex number conjugate of complex number).
\((\mathrm{iv})\;\mathrm{Re}(\mathrm Z)\leq\left|\mathrm Z\right|\;\mathrm{and}\;\mathrm{Im}(\mathrm Z)\leq\left|\mathrm Z\right|\)
proofs:
Let Z = a + ib and it conjugate be \(\left|\overline{\mathrm Z}\right|=\mathrm a-\mathrm{ib}\), and W = c + id be another complex number.
\((\mathrm i)\;\left|\mathrm Z\right|=\left|\overline{\mathrm Z}\right|\)
The absolute value of complex number \(\left|\mathrm Z\right|\) is equal to the absolute value of its conjugate \(\left|\overline{\mathrm Z}\right|\)
⇒ By definition \(\left|\mathrm Z\right|=\sqrt{\mathrm a^2+\mathrm b^2}\)−−−−−−>eqn(i)
⇒ similarly, the absolute value of conjugate of complex number Z is \(\left|\overline{\mathrm Z}\right|=\sqrt{\mathrm a^2+{(-\mathrm b)}^2}\)
⇒ \(\left|\overline{\mathrm Z}\right|=\sqrt{\mathrm a^2+{(\mathrm b)}^2}\)−−−−−−>eqn(ii) [The square of real number is always positive]
Equating the eqn(i) and eqn(ii) we get,
∴ \(\left|\mathrm Z\right|=\left|\overline{\mathrm Z}\right|\)
\((\mathrm{ii})\;\left|\mathrm Z\right|=0\;\mathrm{if}\;\mathrm z=0\)
The absolute value of complex number is zero i.e.\(\left|\mathrm Z\right|=0\) only when the complex number Z itself is zero.
⇒ By definition \(\left|\mathrm Z\right|=\sqrt{\mathrm a^2+\mathrm b^2}\)
⇒ \(0=\sqrt{\mathrm a^2+\mathrm b^2}\) [considering \(\left|\mathrm Z\right|=0\)]
⇒ \(0=\left(\mathrm a^2+\mathrm b^2\right)\) [By multiplying \(\left(\sqrt{\mathrm a^2+\mathrm b^2}\;\right)\) on both sides]
⇒ The sum of two squares of the real and imaginary parts is zero, which only possible when a =0 and b = 0
∴ The complex number Z must be zero i.e. Z = 0
\((\mathrm{iii})\;\left|\mathrm Z.\mathrm W\right|=\left|\mathrm Z\right|.\left|\mathrm W\right|\)
⇒ By the definition of the absolute value of complex number we can write \(\left|\mathrm Z\right|=\sqrt{\mathrm a^2+\mathrm b^2}\)−−−>eqn(i) and \(\left|\mathrm W\right|=\sqrt{\mathrm c^2+\mathrm d^2}\)−−−>eqn(ii)
⇒ \(\mathrm Z.\mathrm W=(\mathrm{ac}-\mathrm{bd})+\mathrm i(\mathrm{ad}+\mathrm{bc})\) [By the multiplication rule of complex numbers]
⇒ \(\left|\mathrm Z.\mathrm W\right|=\sqrt{{(\mathrm{ac}-\mathrm{bd})}^2+{(\mathrm{ad}+\mathrm{bc})}^2}\) [By the definition of the absolute value of complex numbers]
⇒ \(\left|\mathrm Z.\mathrm W\right|=\sqrt{(\mathrm a^2\mathrm c^2+\mathrm b^2\mathrm c^2+\mathrm a^2\mathrm d^2+\mathrm b^2\mathrm d^2)}\) [After simplifying]
⇒ \(\left|\mathrm Z.\mathrm W\right|=\sqrt{\mathrm c^2(\mathrm a^2+\mathrm b^2)+\mathrm d^2(\mathrm a^2+\mathrm b^2)}\) [Taking common factors c² and d²]
⇒ \(\left|\mathrm Z.\mathrm W\right|=\sqrt{(\mathrm a^2+\mathrm b^2)+(\mathrm c^2+\mathrm d^2)}\) [Taking common factors (a² + b²)
⇒ \(\left|\mathrm Z.\mathrm W\right|=\sqrt{(\mathrm a^2+\mathrm b^2)}\;.\;\sqrt{(\mathrm c^2+\mathrm d^2)}\) [By the property of the law of indices]
∴ \(\left|\mathrm Z.\mathrm W\right|=\left|\mathrm Z\right|.\left|\mathrm W\right|\) [from eqn(i) and eqn(ii)]
\(\displaystyle(\mathrm{iv})\;\left|\frac{\mathrm W}{\mathrm Z}\right|=\frac{\left|\mathrm W\right|}{\left|\mathrm Z\right|}\;\mathrm{if}\;\left|\mathrm Z\right|\neq0\)
⇒ \(\displaystyle\frac{\mathrm W}{\mathrm Z}=\left(\frac{\mathrm{ac}+\mathrm{bd}}{\mathrm a^2+\mathrm b^2},\;\frac{\mathrm i(\mathrm{ad}-\mathrm{bc})}{\mathrm a^2+\mathrm b^2}\right)\) [By the division rule of complex numbers]
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\sqrt{\left(\frac{\mathrm{ac}+\mathrm{bd}}{\mathrm a^2+\mathrm b^2}\right)^2+\;\left(\frac{\mathrm{ad}-\mathrm{bc}}{\mathrm a^2+\mathrm b^2}\right)^2}\) [By the definition of absolute value of complex numbers]
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\sqrt{\frac{\mathrm a^2\mathrm c^2+\mathrm b^2\mathrm c^2+\mathrm a^2\mathrm d^2+\mathrm b^2\mathrm d^2}{{(\mathrm a^2+\mathrm b^2)}^2}}\) [After simplifying]
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\sqrt{\frac{\mathrm c^2(\mathrm a^2+\mathrm b^2)+\mathrm d^2(\mathrm a^2+\mathrm b^2)}{{(\mathrm a^2+\mathrm b^2)}^2}}\) [Taking common factors c² and d²]
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\sqrt{\frac{(\mathrm a^2+\mathrm b^2)(\mathrm c^2+\mathrm d^2)}{{(\mathrm a^2+\mathrm b^2)}^2}}\) [Taking common factors (a² + b²)
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\sqrt{\frac{(\mathrm c^2+\mathrm d^2)}{(\mathrm a^2+\mathrm b^2)}}\) [By the multiplicative inverse property]
⇒ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\frac{\sqrt{(\mathrm c^2+\mathrm d^2)}}{\sqrt{(\mathrm a^2+\mathrm b^2)}}\) [By the property of the law of indices]
∴ \(\displaystyle\left|\frac{\mathrm W}{\mathrm Z}\right|=\frac{\left|\mathrm W\right|}{\left|\mathrm Z\right|}\) [By the definition of conjugate of complex number]
\(\\[0.3cm]\)


