Combination

The process of arranging elements, where the order of objects selected doesn’t matter, is known as combination.

Consider a scenario: suppose you have three fruits—mango, orange, and banana—and you’re tasked with blending them to make juice. How many distinct flavors can you create?

Permutation theory tells us that there are six possible orders for these fruits: MOB, MBO, OMB, OBM, BMO, and BOM. Here, we can see tree diagram:

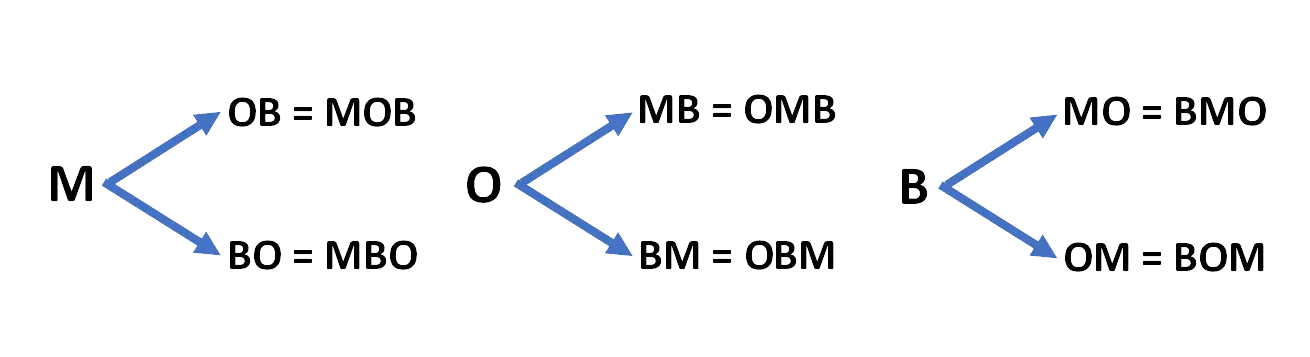
However, regardless of the order, the resulting juice flavor remains the same → just one. Therefore, all six orders are essentially equivalent, representing just one unique combination. Let’s take ‘MBO’ as an example; it encapsulates the fundamental concept of combination.

Note that: combination is an arrangement where the different order of each distinct set have the same meaning. Here are some scenarios that illustrate this fact:

Fails in exam: find the number of way to fail 2 subjects out of 4 subjects.

• In this scenario, the ordering of (each distinct 2 subjects) doesn’t matter. whether you fail (math) & (physics) OR (physics) & (math), it has same meaning.

Choosing a Committee: In a class of 10 students, how many ways can you choose a committee of 4 students?

• same concept applies: the order of students doesn’t matter within (each distinct Committee of 4 students) because it has same meaning.

Drawing Cards: How many ways can you draw 5 cards from a standard deck of 52 cards?

• The order of cards within (each distinct collection of 5 cards) doesn’t matter. This ordering doesn’t affect the gameplay, so it has same meaning.

This is why we don’t care about the ordering of elements in combination. Here, the

• (each distinct 2 subjects),
• (each distinct committee of 4 students),
• (each distinct collection of 5 cards),

represent the meaning of combination.

Relationship between permutation and combination

The relationship between permutation and combination is the key point to deriving the general formula for combination. In the above three scenarios, each distinct set of elements represents the meaning of combination, and the ordering of each distinct set represents the meaning of a permutation.

Note: There is only combination of \(\displaystyle\mathrm n^{\mathrm{th}}\) elements, but for the same \(\displaystyle\mathrm n^{\mathrm{th}}\) elements, the number of permutation is n!.

let’s consider one scenarios for better understanding:

Fails in exam: Find the number of way to fail 2 subjects out of 4 subjects.

Suppose ‘M’ stands for math, ‘P’ for physics, ‘E’ for English, and ‘C’ for computer science.

Here, is the total combination i.e., (The number of way to fail 2 subjects out of 4 subjects) and the permutation of each distinct combination.

As we can see, the number of permutation of each combination is equal to the factorial of the number of elements taken in combination. For example, consider one distinct combination (MP),  which has two element, M and  P. The permutation of this combination is equal to 2! i.e., MP and PM. This is the key relationship between the permutation and combination.
we can now show this relationship in the form of an equation:
\(\displaystyle\;\;\;\;\;\;6\times2!=12\\[0.3cm]\mathrm{or},\;\boxed{\mathrm C(\mathrm n,\;\mathrm r)\times\mathrm r!=\mathrm P(\mathrm n,\;\mathrm r)}\)
This is the relationship between permutation and combination. After further simplification, we get the combination formula:
\(\displaystyle\mathrm{or},\;\mathrm C(\mathrm n,\;\mathrm r)\times\mathrm r!=\frac{\mathrm n!}{(\mathrm n-\mathrm r)!}\\[0.3cm]\mathrm{or},\;\mathrm C(\mathrm n,\;\mathrm r)=\frac{\mathrm n!}{(\mathrm n-\mathrm r)!\times\mathrm r!}\)

Hence, \(\boxed{\boldsymbol\;\mathbf C\boldsymbol(\mathbf n\boldsymbol,\boldsymbol\;\mathbf r\boldsymbol)\boldsymbol=\frac{\mathbf n\boldsymbol!}{\boldsymbol(\mathbf n\boldsymbol-\mathbf r\boldsymbol)\boldsymbol!\boldsymbol\times\mathbf r\boldsymbol!}}\) is the general formula for combinations.

we read \(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)\) as ” The number of combination of ‘n’ elements taken ‘r’ at a time.”

Properties of combination

While there are numerous properties associated with combinations, we will focus on five key properties and their derivation in this discussion. Three properties are mentioned here, while the remaining two are covered in the context of the Binomial theorem in the topic of “properties of binomial coefficients”

1st property

The first property states that:

“The number of combination of n things taken r at a time is equal to the number of combinations of n things taken n – r at a time.”
symbolically: \(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm n-r)\)
let’ apply General formula or Combinations on the Right-Hand Side of above equation:

\(\displaystyle\mathrm R.\mathrm H.\mathrm S=\mathrm C(\mathrm n,\;\mathrm n-\mathrm r)\)

After applying the general formula of combinations, we get:

\(\displaystyle=\frac{\mathrm n!}{\lbrack\mathrm n-(\mathrm n-\mathrm r)\rbrack!\times(\mathrm n-\mathrm r)!}\\[0.3cm]=\frac{\mathrm n!}{(\cancel{\mathrm n}-\cancel{\mathrm n}+\mathrm r)!\times(\mathrm n-\mathrm r)!}\\[0.3cm]=\frac{\mathrm n!}{\mathrm r!\times(\mathrm n-\mathrm r)!}\\[0.3cm]=\mathrm C(\mathrm n,\;\mathrm r)=\mathrm L.\mathrm H.\mathrm S\;\mathrm{Proved}\)
Therefore, \(\displaystyle\boxed{\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm n-\mathrm r)}\)

2nd property

The second property states that:

\(\displaystyle\mathrm{If}\;\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm r’)\;\mathrm{then},\;\mathrm{either}\;\mathrm r’=\mathrm n-\mathrm r\;\mathrm{or}\;\mathrm r=\mathrm r’\)

Rather then a property, it’s a relation between the general formula of combinations and the 1st property. let’s consider these as eqn(a) and eqn(b) respectively:

\(\displaystyle\boxed{\mathrm C(\mathrm n,\;\mathrm r)=\frac{\mathrm n!}{(\mathrm n-\mathrm r)!\times\mathrm r!}}\Rightarrow\mathrm{eqn}(\mathrm a)\) and \(\displaystyle\boxed{\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm n-\mathrm r)}\Rightarrow\mathrm{eqn}(\mathrm b)\)

\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm r’)\)
This relation is only true when \(\displaystyle\mathrm r’=\mathrm n-\mathrm r\) because after substitution, we arrive at eqn(b):
\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm n-\mathrm r)\)
This is true according to our eqn (b), i.e., the 1st property

Again,

\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm r’)\)
In another way, this relation can be true when \(\displaystyle\mathrm r’=\mathrm r\) because after substitution, we arrive at L.H.S = R.H.S:
\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm r)\)

Therefore, \(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\mathrm C(\mathrm n,\;\mathrm r’)\;\mathrm{when},\;\mathrm{either}\;\mathrm r’=\mathrm n-\mathrm r\;\;\;\mathrm{OR}\;\;\;\;\mathrm r=\mathrm r’\)

3rd property

The 3rd property states that:

\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)+\mathrm C(\mathrm n,\;\mathrm r-1)=\mathrm C(\mathrm n+1,\;\mathrm r)\)

we can write the L.H.S as

\(\displaystyle\mathrm C(\mathrm n,\;\mathrm r)=\frac{\mathrm n!}{(\mathrm n-\mathrm r)!\times\mathrm r!}\;\;\;\;\;\mathrm{and}\;\;\;\;\;\;\mathrm C(\mathrm n,\;\mathrm r-1)=\frac{\mathrm n!}{(\mathrm n-\mathrm r+1)!\times(\mathrm r-1)!}\)

This is just applying general formula for combinations, Now, adding them together, we get the result:

\(\\[0.3cm]\)

«Previous page

MCQs on combination